7 ПЕРЕСМОТРЕННЫЙ АЛГОРИТМ ЕВКЛИДА
Рискуя наскучить моим читателям, я посвящу еще одну главу алгоритму Евклида. Полагаю, что к этому времени некоторые из читателей уже закодируют его в виде
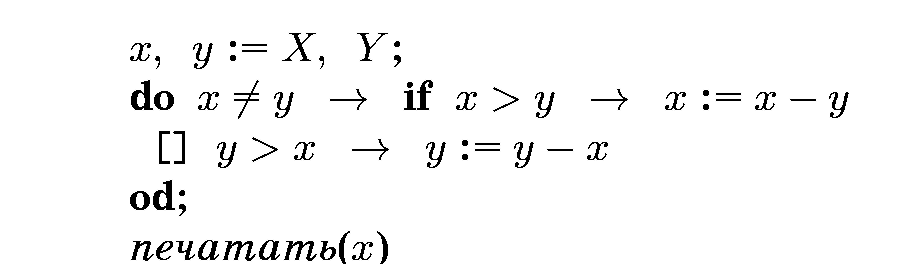
где предохранитель конструкции повторения гарантирует, что конструкция выбора не приведет к отказу. Другие читатели обнаружат, что этот алгоритм можно закодировать более просто следующим образом:
Попробуем теперь забыть игру на листе картона и попытаемся изобрести заново алгоритм Евклида для отыскания наибольшего общего делителя двух положительных чисел X и Y. Когда мы сталкиваемся с такого рода проблемой, в принципе всегда возможны два подхода.
Первый состоит в том, чтобы пытаться следовать определению требуемого ответа настолько близко, насколько это возможно. По-видимому, мы могли бы сформировать таблицу делителей числа
X; эта таблица содержала бы только конечное число элементов, среди которых имелись бы 1 в качестве наименьшего и X в качестве наибольшего элемента. (Если X = 1, то наименьший и наибольший элементы совпадут. Затем мы могли бы сформировать также аналогичную таблицу делителей Y. Из этих двух таблиц мы могли бы сформировать таблицу чисел, присутствующих в них обеих. Она представляет собой таблицу общих делителей чисел X и Y и обязательно является непустой, так как содержит элемент 1. Следовательно, из этой третьей таблицы мы можем выбрать (поскольку она тоже конечная!) максимальный элемент, и он был бы наибольшим общим делителем.Иногда близкое следование определению, подобное обрисованному выше, является лучшим из того, что мы можем сделать. Существует, однако, и другой подход, который стоит испробовать, если мы знаем (или можем узнать) свойства функции, подлежащей вычислению. Может оказаться, что мы знаем так много свойств, что они в совокупности определяют эту функцию, тогда мы можем попытаться построить ответ, используя эти свойства.
В случае наибольшего общего делителя мы замечаем, например, что, поскольку делители числа —х
те же самые, что и для самого числа х, НОД(ж, у) определен также для отрицательных аргументов и не меняется, если мы изменяем знак аргументов. Он определен и тогда, когда один из аргументов равен нулю; такой аргумент обладает бесконечной таблицей делителей (и поэтому нам не следует пытаться строить эту таблицу!), но поскольку второй аргумент (^ 0) обладает конечной таблицей делителей, таблица общих делителей является все же непустой и конечной. Итак, мы приходим к заключению, что НОД(ж, у) определен для всякой пары (ж, у), такой, что (ж, у) ^ (О,0). Далее, в силу симметрии понятия "общий" наибольший общий делитель является симметричной функцией своих двух аргументов. Еще одно небольшое умственное усилие позволит нам убедиться в том, что наибольший общий делитель двух аргументов не изменяется, если мы заменяем один из этих аргументов их суммой или разностью. Объединив все эти результаты, мы можем записать: для (ж, у) ^ (О, О)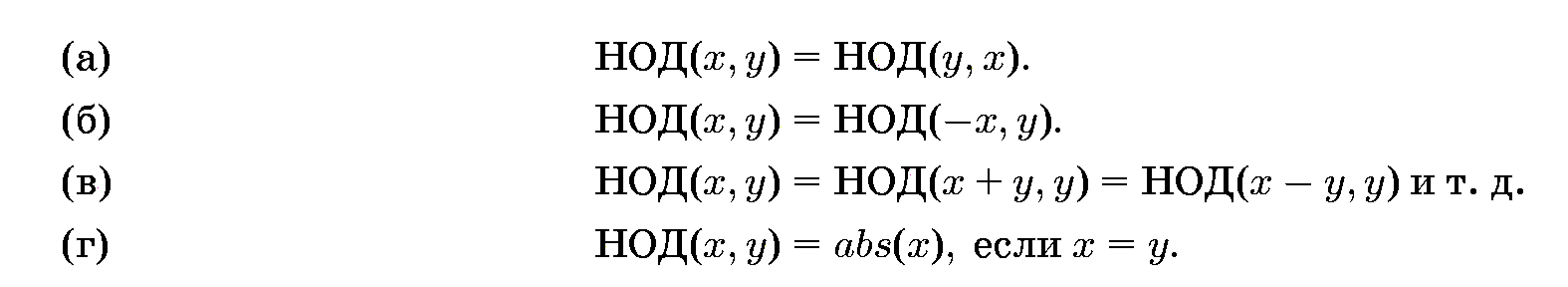
Предположим для простоты рассуждений, что этими четырьмя свойствами исчерпываются наши познания о функции ПОД. Достаточно ли их? Вы видите, что первые три отношения выражают наибольший общий делитель чисел хну через ПОД для другой пары, а последнее свойство выражает его непосредственно через ж. И в этом уже просматриваются контуры алгоритма, который для начала обеспечивает истинность
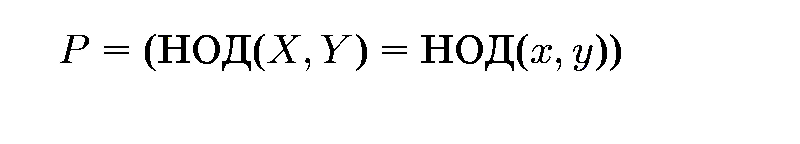
(это легко достигается путем присваивания "
х,у := X,Y"), после чего мы "утрамбовываем" пару значений (ж, у) таким образом, чтобы в соответствии с (а), (б) или (в) отношение Р оставалось инвариантным. Если мы можем организовать этот процесс утрамбовки так, чтобы достигнуть состояния, удовлетворяющего х = у, то, согласно (г), мы находим искомый ответ, взяв абсолютное значение х.Поскольку наша конечная цель состоит в том, чтобы обеспечить при инвариантности
Р истинность х = у, мы могли бы испытать в качестве монотонно убывающей функции функцию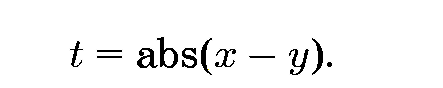
Чтобы упростить наш анализ (всегда похвальная цель!), мы отмечаем, что если начальные значения хну неотрицательные, то ничего нельзя выиграть введением отрицательного значения: если присваивание х := Е обеспечило бы х < О, то присваивание х := —Е никогда не привело бы к получению большего конечного значения t (потому, что у > 0). Поэтому мы усиливаем наше отношение Р, которое должно сохраняться инвариантным:
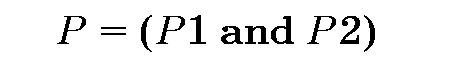
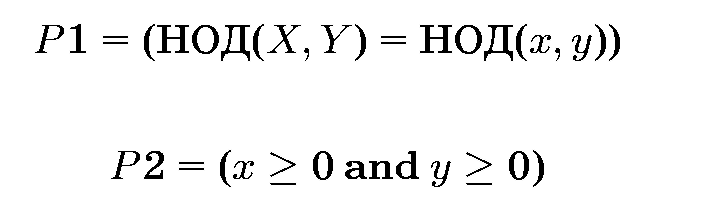



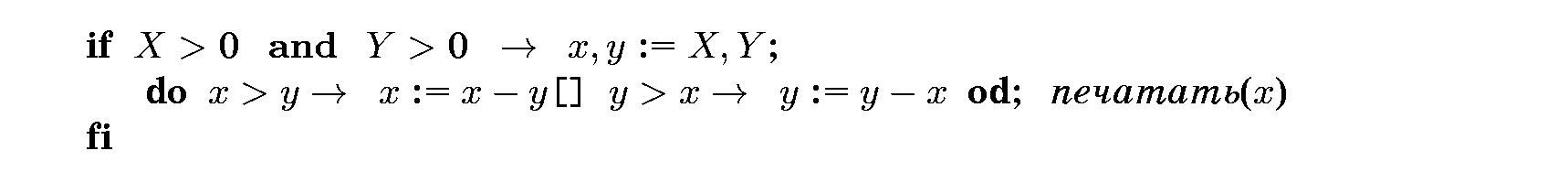
Включив только один вариант в конструкцию выбора, мы явно выразили условия, при которых ожидается работа этой маленькой программы. В таком виде это хорошо защищенный и довольно самостоятельный фрагмент, обладающий тем приятным свойством, что попытка запуска вне его области определения приведет к немедленному отказу.